MATEMATIKA

Macam bangun datar

Jenis bangun datar bermacam-macam, antara lain persegi, persegi panjang, segitiga, jajar genjang, trapesium, layang-layang, belah ketupat, dan lingkaran.
Nama-nama Bangun Datar

• Persegi Panjang, yaitu bangun datar yang mempunyai sisi berhadapan yang sama panjang, dan memiliki empat buah titik sudut siku-siku.
• Persegi, yaitu persegi panjang yang semua sisinya sama panjang.
• Segitiga, yaitu bangun datar yang terbentuk oleh tiga buah titik yang tidak segaris
• Jajar Genjang, yaitu segi empat yang sisinya sepasang-sepasang sama panjang dan sejajar.
• Trapesium, yaitu segi empat yang memiliki tepat sepasang sisi yang sejajar.
• Layang-layang, yaitu segi empat yang salah satu diagonalnya memotong tegak lurus sumbu diagonal lainnya.
• Belah Ketupat, yaitu segi empat yang semua sisinya sama panjang dan kedua diagonalnya saling berpotongan tegak lurus.
• Lingkaran, yaitu bangun datar yang terbentuk dari himpunan semua titik persekitaran yang mengelilingi suatu titik asal dengan jarak yang sama. jarak tersebut biasanya dinamakan r, atau radius, atau jari-jari.

[sunting] Rumus bangun datar

Rumus Bangun Datar

• Rumus Persegi

Luas = s x s = s²

Keliling = 4 x s

dengan s = panjang sisi persegi

• Rumus Persegi Panjang

Luas = p x l

Keliling = 2p + 2l = 2 x (p + l)

dengan p = panjang persegi panjang, dan l = lebar persegi panjang

• Rumus Segitiga

Luas = ½ x a x t

dengan a = panjang alas segitiga, dan t = tinggi segitiga

Panjang sisi miring segitiga siku-siku dicari dengan rumus Phytagoras (A² + B² = C²)

• Rumus Jajar Genjang

Luas = a x t

dengan a = panjang alas jajargenjang, dan t = tinggi jajargenjang

• Rumus Trapesium

Luas = ½ x (s1 + s2) x t

dengan s1 dan s2 = sisi-sisi sejajar pada trapesium, dan t = tinggi trapesium

• Rumus Layang-layang

Luas = ½ x diagonal (d) 1 x diagonal (d) 2

• Rumus Belah Ketupat

Luas = ½ x diagonal (d) 1 x diagonal (d) 2

• Rumus Lingkaran

Luas = π (pi) x jari-jari (r)

Sifat-sifat bangun datar

• Layang-layang = terbagi atas 2 digonal yang berbeda ukurannya
• Persegi = semua sisi-sisinya sama panjang, semua sudut sama besar
• Persegi panjang = sisi yang behadapan sama panjang, semua sudut sama besar
• Belah ketupat = semua sisi-sisinya sama panjang, sudut yang berhadapan sama besar
• Jajar genjang = sisi yang berhadapan sama panjang, sudut yang berhadapan sama besar
• Lingkaran = mamiliki simetri lipat dan simetri putar yang tak terhingga jumlahnya

.

Pengertian Balok

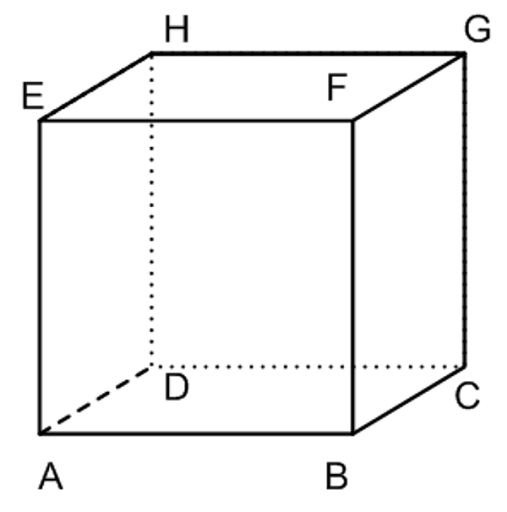
Balok adalah bangun ruang yang dibentuk oleh tiga pasang persegi panjang dimana tiap pasang persegi panjang mempunyai bentuk dan ukuran yang sama dan persegipanjang yang sehadap adalah kongruen. Tiga pasang persegi panjang inilah disebut sisi-sisi balok. Berkut adalah gambar balok ABCD.EFGH

 

Sama halnya dengan kubus balok juga memiliki unsur-unsur sebagai berikut:

a. Sisi/Bidang

Sisi balok adalah bidang yang membatasi suatu balok. Balok ABCD.EFGH memiliki 6 buah sisi berbentuk persegi panjang yaitu sisi bawah = ABCD, sisi atas = EFGH, sisi depan = ABFE, sisi belakang = DCGH, sisi samping kanan = ADHE , dan sisi samping kiri  = BCGF.
Keenam sisi balok diatas saling berpasangan sehingga membentuk 3 pasang sisi yang saling   berhadapan yang sama bentuk dan besarnya yaitu ABFE berpasangan dengan DCGH, ABCD dengan EFGH, dan BCGF dengan ADHE.

b. Rusuk

Garis potong sisi-sisi pada blok dinamakan rusuk. Balok  ABCD.EFGH memiliki 12 rusuk yaitu AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, dan HD.

c. Titik Sudut

Titik temu antara tiga buah rusuk pada balok disebut titik sudut balok. Balok ABCD.EFGH memiliki 8 titik sudut, yaitu A, B, C, D, E, F, G, dan H.

d. Diagonal sisi/bidang

Garis yang menghubungkan dua titik sudut yang berhadapan pada sisi balok disebut diagonal sisi/bidang. Terdapat 12 buah diagonal sisi pada balok ABCD.EFGH yaitu AC, BD, EG, HF, AF, BE, CH, DG, AH, DE, BG, CF.

 e. Diagonal Ruang

Ruas garis yang menghubungkan dua titik sudut yang saling berhadapan di dalam balok disebut diagonal ruang. Terdapat 4 buah diagonal ruang pada balok ABCD.EFGH yaitu AG, BH, CE,dan AF. Keempat diagonal ruang ini saling berpotongan ditengah-tengah.

f. Bidang Diagonal

Bidang yang dibentuk oleh dua buah diagonal bidang yang sejajar dan dua buah rusuk balok yang saling sejajar disebut bidang diagonal.  Terdapat 6 buah bidang diagonal pada balok ABCD.EFGH yaitu ACGE, BDHF, ABGH, CDEF, ADGF, BCHE.

Sifat-sifat Balok

Balok memiliki sifat-sifat sebagai berikut

1. Setiap sisi balok berbentuk persegi panjang.
2. Setiap rusuk-rusuk yang sejajar memiliki ukuran sama panjang.
3. Setiap diagonal bidang pada sisi yang berhadapan memiliki ukuran sama panjang.
4. Setiap diagonal ruang pada balok memiliki ukuran sama panjang.
5. Setiap bidang diagonal pada balok memiliki bentuk persegipanjang.

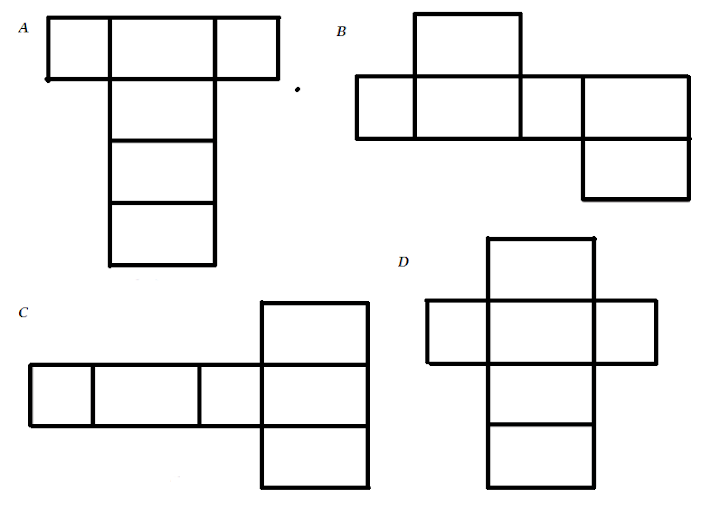
Jaring-Jaring Balok

Untuk menemukan rangkaian jaring-jaring balok dilakukan dengan cara memotong rusuk-rusuk balok. Jaring-jaring balok terbentuk dari rangkaian enam persegi panjang. Rangkaian jaring-jaring balok terdiri dari tiga pasang persegi panjang yang memiliki bentuk dan ukuran yang sama dengan pasangannya. Bentuknya ada berbagai macam. Tapi perlu diingat bahwa tidak semua rangakaian persegi panjang bisa membentuk balok. Beberapa contoh jaring-jaring balok seperti gambar berikut:

 

Rumus Balok

1. Volume Balok

Untuk mencari volume  sebuah balok digunakan rumus V= Luas alas x tinggi. Misalkan untuk menghitung volume balok ABCD.EFGH, dimana Luas alas balok = p x l.
Sehingga diperoleh
Volum balok = Luas alas balok x  tinggi
                    = p x l x  t
Jadi, volume balok dapat dinyatakan sebagai berikut.

V. Balok = p x l x t

 2. Luas Permukaan Balok

Untuk mengetahui luas permukaan digunakan rumus, misalnya balok  ABCD.EFGH.
Luas Permukaan balok ABCD.EFGH = 2 Luas ABCD + 2 Luas ABFE + 2 Luas ADHE

= 2 pl + 2 pt + 2 lt

Jadi, luas permukaan kubus dapat dinyatakan dengan rumus sebagai berikut.

Luas permukaan balok = 2(pl + lt + pt)

Contoh Soal

1. Diketahui sebuah balok memiliki ukuran seperti gambar dibawah ini.

AB = p = 10 cm

BC = l = 3 cm
CG = t = 4 cm



Tentukan:

1. volume balok.
2. luas permukaan balok,
   

     Penyelasaian

1. V. Balok ABCD.EFGH = p x l x t

= 10 cm x 3 cm x 4 xm

= 120 cm³

2. Luas permukaan balok ABCD.EFGH = 2(pl + lt + pt)

= 2 (10 . 3 + 3 . 4 + 10 . 4)

= 2 (30 + 12 + 40)

= 2 . 82

= 164 cm²

Bola

Perhatikan gambar di samping. Mengapa dalam olahraga bowling, benda yang dilemparkan berbentuk bola? Apakah kelebihannya sehingga benda-benda berbentuk bola digunakan dalam olahraga sepak bola, bola voli, bowling, dan billiard? Agar dapat lebih mengenal bangun bola, pelajarilah materi berikut ini.

1. Unsur-unsur Bola

Perhatikan gambar berikut.

Suatu lingkaran diputar setengah putaran dengan diameter sebagai sumbu putarnya akan diperoleh bangun ruang seperti gambar 2.10 (b). Bentuk bangun yang demikian disebut bola dengan jari-jari bola r dan tinggi d.

2. Menghitung Luas Selimut dan Volume Bola

Sebelum mempelajari luas selimut dan volume bola, lakukanlah kegiatan berikut.

Ternyata dari kegiatan di atas kita dapat merumuskan luas selimut atau permukaan (sisi) bola. Jika jari-jari alas tabung tersebut r dan tingginya sama dengan diameter d, maka luas selimut atau sisi bola dengan jari-jari r adalah:

D. Hubungan Volume Bangun Ruang Sisi Lengkung dengan Jari-jari

Pada rumus mencari volume bangun ruang sisi lengkung, semua tergantung pada unsur-unsur bangun tersebut, misalnya jari-jari dan tinggi bangun tersebut.

1. Perbandingan Volume Tabung, Kerucut, dan Bola karena Perubahan Jari-jari

a. Perbandingan Volume Tabung
Apabila ada dua buah tabung dengan tinggi yang sama, tetapi jari-jari berbeda, maka perbandingan kedua volume tabung sama dengan perbandingan kuadrat masing-masing jari-jarinya.

b. Perbandingan Volume pada Kerucut
Apabila ada dua buah kerucut dengan tinggi sama, tetapi jari-jari alasnya berbeda, maka perbandingan volume kedua kerucut dengan perbandingan kuadrat masing-masing jari-jarinya.

c. Perbandingan Volume pada Bola
Apabila ada dua buah bola dengan jari-jari yang berbeda, maka perbandingan volumenya sama dengan perbandingan di pangkat tiga dan masing-masing jari-jarinya.

 

Pernahkah anda memainkan permainan ular tangga atau monopoli? Dalam permainan tersebut ada sebuah benda  berbentuk kotak yang  selalu digunakan. Ya betul, benda itu disebut dadu. Atau pernahkah anda memainkan permainan asah otak di samping? Terus kaitannya dengan pembahasan kita kali ini? Kaitannya adalah dadu dan rubik cube merupakan salah satu contoh kubus yang dapat kita jumpai dalam kehidupan sehari. Masih banyak lagi contoh yang lain.

Pengertian Kubus

Kubus merupakan salah satu bentuk bangun ruang atau dimensi tiga. Kubus merupakan sebuah bangun ruang atau dimensi tiga yang semua sisinya berbentuk persegi dan semua rusuknya sama panjang. Coba kita perhatikan gambar berikut:

Gambar diatas dinamakan kubus ABCD.EFGH. Dari gambar diatas tampak bahwa kubus memiliki unsur-unsur sebagai berikut :

• Sisi/Bidang kubus merupakan datar yang membatasi kubus. Kubus memiliki 6 buah sisi yang semuanya berbentuk persegi, yaitu sisi bawah = ABCD, sisi atas = EFGH, sisi depan (ABFE), sisi belakang= CDHG, sisi kanan = ADHE, dan sisi kiri = BCGF.
• Rusuk  merupakan garis potong antara dua sisi bidang kubus. Kubus memiliki 12 buah rusuk, yaitu AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, dan DH.
• Titik Sudut merupakan titik potong antara tiga rusuk. Kubus ABCD. EFGH memiliki 8 buah titik sudut, yaitu titik A, B, C, D, E, F, G, dan H.
• Diagonal Bidang merupakan garis yang menghubungkan dua titik sudut yang saling berhadapan dalam satu sisi/bidang. Pada kubus ABCD.EFGH terdapat 8 buah titik sudut yaitu : A, B, C, D, E, F, G, H, .
• Diagonal ruang merupakan HB yang menghubungkan dua titik sudut yang saling berhadapan dalam satu ruang. Terdapat empat diagonal ruang yang sama panjangnya dan saling berpotongan di tengah-tenagh yaitu AG = BH = CE = DF.
• Bidang diagonal merupakan bidang yang dibentuk oleh dua diagonal bidang dan dua rusuk yang saling sejajar. Terdapat 6 buah bidang diagonal yaitu : ACGE, BDHF, ABGH, CDEF, ADGF, BCHE.

Sifat-sifat Kubus

Kubus memiliki sifat-sifat sebagai berikut:

• Semua sisi merupakan persegi
• Semua rusuk sama panjang
• Semua diagonal bidang sama panjang
• Semua diagonal ruang sama panjang
• Semua bidang diagonal berbentuk persegi panjang.

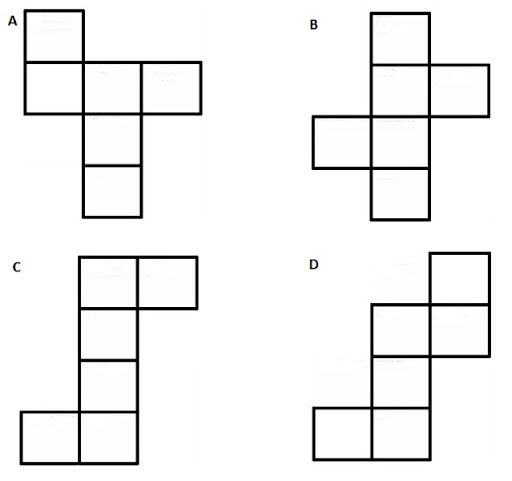
Jaring-jaring kubus

Jaring-jaring kubus dibentuk dari 6 buah persegi yang apabila dirangkaikan akan membentuk suatu kubus. Ada beberapa macam bentuk jaring-jaring kubus, diantaranya tampak seperti gambar berikut.

Rumus-rumus Kubus

1. Volume kubus

Pada dasarnya untuk mencari volume suatu bidang ruang digunakan rumus
Volume  = Luas alas x tinggi
Dimana luas alas kubus adalah persegi dan panjang sisi alasnya sama dengan tinggi kubus
Sehingga:
volume kubus = panjang rusuk × panjang rusuk × panjang rusuk

= s × s × s

= s³

Jadi, volume kubus dapat dinyatakan sebagai berikut.

V = s³

2. Luas Permukaan

Untuk mencari luas permukaan kubus, kita akan  menghitung luas jaring-jaring kubus yang berjumlah 6 buah persegi yang sama besar dan kongruen. Sehingga :

Luas permukaan kubus = luas jaring-jaring kubus
= 6 × (s × s)
= 6 × s2
= 6 s²
Jadi, luas permukaan kubus dapat dinyatakan dengan rumus sebagai berikut.

L = 6s²

Contoh soal

1. ABCD.EFGH adalah kubus dengan panjang rusuk 5 cm. Hitunglah volume dan luas permuakaan bangun tersebut!

Penyelesaian:

V Kubus ABCD.EFGH = s³

                                = (5 cm)³

                                = 125 cm³

Luas permukaan kubus = 6 s²

                                = 6 (5 cm)²

                                = 150 cm²

 2. Hitunglah panjang rusuk suatu kubus jika diketahui memiliki jaring-jaring kubus dengan luas 294 cm²!

Penyelesaian:

Luas permukaan kubus = 6s²

Diperoleh           294 = 6 · s2

s2 = 294

          6

s2  = 49

s    = 7

Jadi, panjang rusuk kubus tersebut adalah 7 cm.